树和二叉树

发表于 | 阅读量 次 | 分类于 |

前言

树是数据元素（结点）之间具有层次关系的非线性结构。在树结构中，除根以外的结点只有一个前驱结点，可以有零至多个后继结点，根结点没有前驱结点

基本术语

Alt text
1.父母、孩子、兄弟结点
2.度（结点所拥有的子树数目），如A的度为3
3.结点的层次（结点处于树中的位置，约定根结点层次为1），树的高度（树中结点的最大层次数）如图中树高度为3
4.边（设X结点是y结点的父母结点，有序对（X，y）称为这两个结点的边，路径如A到E结点，表示为（A，B，E），路径长度（路径上的边数）为2
5.无序数与有序树（区别子树之间有没有次序）
6.森林（删除根结点）

二叉树性质

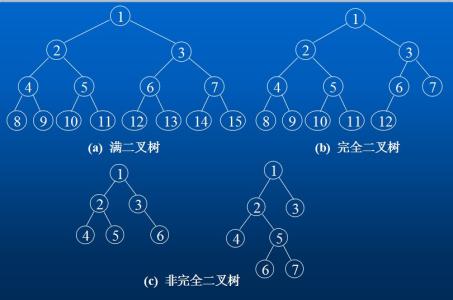
Alt text
二叉树最多有两颗子树，分别为左右子树
性质1：若根结点的层次为1，则二叉树第i层最多有2^(i-1)(i>1)个结点
性质2：在高度为h的二叉树中，最多有2^h-1个结点（h>=0)
性质3：设一棵二叉树的叶子结点数为n0,2度结点数为n2，则n0=n2+1
性质4：一颗具有n个结点的完全二叉树，其高度为h=[log以2为底数n为参数]+1；其中[]是高斯取整函数
性质5：一颗具有n个结点的完全二叉树，对序号为i（0<=i0，则i的父母结点序号为[(i+1)/2]
2.若2i+1<n，则i的左孩子结点序号为2i+1；否则无左孩子
3.若2i+2<n，则i的右孩子结点序号为2i+2，否则i无右孩子

二叉树的遍历规则

孩子优先遍历
二叉树的遍历是按照一定规则和次序访问二叉树中的所有结点，并且每个结点仅被访问一次，同时遍历二叉树访问结点的次序是线性的。
1.先根次序：访问根结点，遍历左子树，遍历右子树（124536）
2.中根次序：遍历左子树，访问根结点，遍历右子树（425136）
3.后根次序：遍历左子树，遍历右子树，访问根结点（452631）

兄弟优先遍历
该遍历是按照层次进行的，遍历历程是从根结点开始，逐层深入，从左至右依次访问完当前层的所有结点，在访问下一层

二叉树抽象数据类型和存储结构

顺序存储结构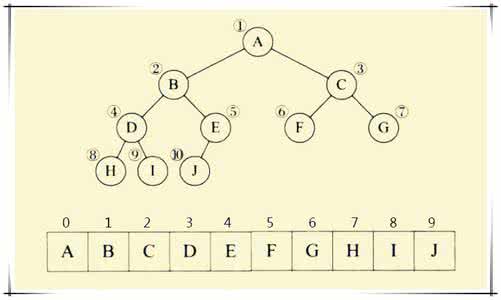
Alt text
二叉树的顺序存储结构仅适用于完全二叉树和满二叉树，如图所示。根据之前的性质，可以实现对应关系一一对应个。
而对于非完全二叉树，如果采取顺序存储，可以将其补成一个完全二叉树，对于空结点利用特殊符号代替，但是会造成空间浪费，并且线性映射关系不明确

链式存储结构
Alt text
二叉链表采用两条链分别连接左右孩子结点，每个结点有三个域：data存储数据元素，left、right分别指向左右孩子结点
三叉链表在二叉链表基础上增加一条链parent连接父母结点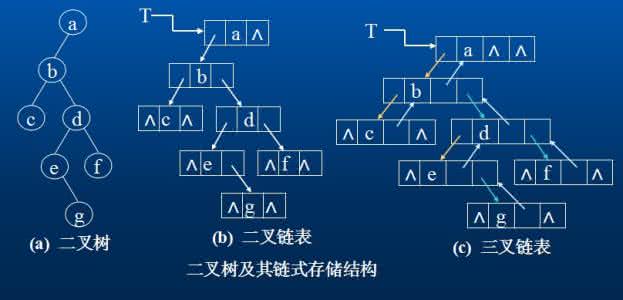
Alt text

二叉链表结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class BinaryNode<T> {
	public T data;                 //数据域，存储数据元素
	public BinaryNode<T> left,right;   //链域，分别指向左、右孩子结点
	
	public BinaryNode(T data,BinaryNode<T> left,BinaryNode<T> right){
		this.data=data;
		this.left=left;
		this.right=right;
	}
	
	public BinaryNode(T data){
		this(data,null,null);
	}
	
	public BinaryNode(){
		this(null,null,null);
	}
}

抽象数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public interface BinaryTTree<T> {
	boolean isEmpty();           //判断二叉树是否为空
	int count();                 //返回二叉树的结点个数
	int height();                //返回二叉树的高度
	void preOrder();             //先根次序遍历二叉树
	void inOrder();              //中根次序遍历二叉树
	void postOrder();            //后根次序遍历二叉树
	void levelOrder();           //按层次遍历二叉树
	BinaryNode<T> search(T key);   //查找并返回首次出现关键字为key元素结点
	BinaryNode<T> getParent(BinaryNode<T> node);      //返回node的父母结点
	void insertRoot(T x);            //插入元素x作为根结点
	BinaryNode<T> insertChild(BinaryNode<T> p,T x,boolean leftChild); //插入孩子节点
	void removeChild(BinaryNode<T> p,boolean leftChild); //删除p结点的左或右子树
	void removeAll();  //删除二叉树
}

下面是其实现类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
public class BinaryTree<T> implements BinaryTTree<T>{
	public BinaryNode<T> root;   //根结点，结点结构为二叉链表
	public BinaryTree(){         //构造空二叉树
		this.root=null;
	}
	public boolean isEmpty() {  //判断二叉树是否为空
		return this.root==null;
	}
	public int count() {
		return count(root);
	}
	
	public int count(BinaryNode<T> p){ //返回以p结点为根的子树的结点个数
		if(p==null)
			return 0;
		return 1+count(p.left)+count(p.right);
	}
	public int height() {
		return height(root);
	}
	public int height(BinaryNode<T> p){
		if(p==null)
			return 0;
		int lh=height(p.left); //返回左子树高度
		int rh=height(p.right); //返回右子树高度
		return (lh>=rh)?lh+1:rh+1; //当前子树高度为较高子树高度加1
	}
	
	public void preOrder() {
		System.out.println("先根次序遍历二叉树:  ");
		preOrder(root);
		System.out.println();
		
	}
	
	public void preOrder(BinaryNode<T> p){
		if(p!=null)
		{
			System.out.println(p.data.toString()+" ");//访问当前结点
			preOrder(p.left); //按先根次序遍历当前结点左子树，递归调用
			preOrder(p.right); //按先根次序遍历当前结点右子树，递归调用
		}
	}
	public void inOrder() {
		System.out.println("中根次序遍历二叉树 :   ");
		inOrder(root);
		System.out.println();	
	}
	public void inOrder(BinaryNode<T> p){
		if(p!=null)
		{
			inOrder(p.left);
			System.out.println(p.data.toString()+" ");
			inOrder(p.right);
		}
	}
	
	public void postOrder() {
	
		System.out.println("后根次序遍历二叉树 :   ");
		inOrder(root);
		System.out.println();
	}
	
	public void postOrder(BinaryNode<T> p){
		if(p!=null){
			postOrder(p.left);
			postOrder(p.right);
			System.out.println(p.data.toString()+" ");
		}
	}
	public void levelOrder() {
		// TODO Auto-generated method stub
		
	}
	public BinaryNode<T> search(T key) {
		return search(root,key);
	}
	
	public BinaryNode<T> search(BinaryNode<T> p,T key) {
		if(p==null||key==null)
			return null;
		if(p.data.equals(key))  //查找成功，返回找到结点
			return p;
		BinaryNode<T> find=search(p.left,key);//在左子树中查找，递归调用
		if(find==null)
			find=search(p.right,key);//左子树中未找到，在右子树中继续递归查找
		return find;
	}
	public BinaryNode<T> getParent(BinaryNode<T> node) {
	if(root==null||node==null||node==root)
		return null;
	 return getParent(root,node);
	}
	
	public BinaryNode<T> getParent(BinaryNode<T> p,BinaryNode<T> node) {
	if(p==null)
		return null;
	if(p.left==node||p.right==node)
		return p;
	BinaryNode<T> find=getParent(p.left,node);
	if(find==null)
		find=getParent(p.right,node);
		return find;
	}
	public void insertRoot(T x) {
		root=new BinaryNode<T>(x, root, null);
		
	}
	//插入元素x作为p结点的孩子，若leftChild为true,插入结点作为左孩子，否则作为右孩子
	public BinaryNode<T> insertChild(BinaryNode<T> p,T x,boolean leftChild){
		if(p==null||x==null)
			return null;
		if(leftChild)
		{
			p.left=new BinaryNode<T>(x, p.left, null);//插入x作为p的左孩子，p原左孩子变为x左孩子
			return p.left;
		}
		p.right=new BinaryNode<T>(x,null,p.right); //插入x结点作为p的右孩子
		return p.right;
	}
	
	public void removeChild(BinaryNode<T> p, boolean leftChild) {
	if(p!=null)
		if(leftChild)
			p.left=null;
		else
			p.right=null;
		
	}
	public void removeAll() {
		this.root=null;
		
	}

快乐源于分享，总结溢于提高

热评文章