栈

前言

栈是一种特殊的线性表，其特殊之处在于插入和删除操作的位置受到限制，而且插入和删除只允许在线性表的一端进行，特点是后进先出

栈抽象数据类型

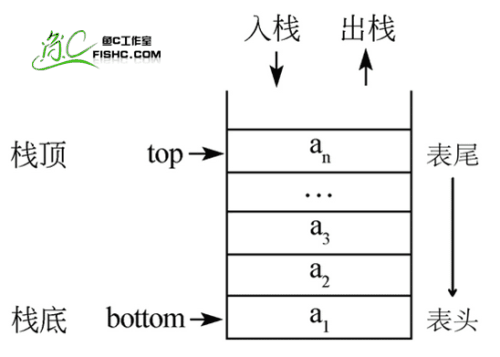
其中允许操作的一端为栈顶（top），不允许操作的一端为栈底（bottom），栈中插入元素的操作称为入栈（push），删除元素的操作为出栈（pop），没有元素的栈称为空栈

public interface SStack<T> {

	boolean isEmpty();  //判断是否为空栈
	void push(T x);     //元素x入栈
	T pop();            //出栈，返回当前栈顶元素
	T get();            //取栈顶元素，未出栈
}

顺序栈

采用顺序存储结构的栈称为顺序栈

public class SeqStack<T> implements SStack<T>{

	private Object element[];    //存取栈数据元素的数组
	private int top;             //栈顶元素下标
	
	public SeqStack(int size){    //构造容量为size的空栈
		this.element=new Object[Math.abs(size)];
		this.top=-1;
	}
	
	public SeqStack(){         //构造默认容量的空栈
		this(64);
	}
	
	public boolean isEmpty() { //判断栈是否为空
		
		return this.top==-1;
	}

	public void push(T x) {    //元素x入栈，空对象不能入栈
		if(x==null)
			return;
		if(this.top==element.length-1)   //栈满，扩充栈容量
		{
			Object[] temp=this.element;
			this.element=new Object[temp.length*2];
			for(int i=0;i<temp.length;i++)
				this.element[i]=temp[i];
		}
		this.top++;
		this.element[this.top]=x;
	}

	public T pop() {  //出栈
		
		return this.top==-1?null:(T)this.element[this.top--];
	}

	public T get() {		//取栈顶元素
		return this.top==-1?null:(T)this.element[this.top];
	}

}

如上，push（），pop（），get（）方法的时间复杂度为O（1），而需要扩充容量时，复杂度为O（n）；

链式栈

采用链式存储结构的栈称为链式栈，这里采用单链表

public class LinkedStack<T> implements SStack<T>{

	private Node<T> top;         //栈顶结点
	
	public LinkedStack(){        //构造空栈
		this.top=null;
	}
	
	public boolean isEmpty() {     //判断栈是否为空
		return this.top==null;
	}

	public void push(T x) {
		if(x!=null)
			this.top=new Node(x, this.top);  //头插入，x结点作为新的栈顶结点
		
	}

	public T pop() {         //出栈，返回栈顶元素
		if(this.top==null)
			return null;
		T temp=this.top.data;
		this.top=this.top.next;
		return temp;
	}

	public T get() {
		return this.top==null?null:this.top.data;
	}

}