线性表之顺序表

发表于 | 阅读量 次 | 分类于 |

前言

数据结构是指数据间存在的关系，通常包含三个方面。数据的逻辑结构（线性结构、树、图），数据的存储结构（顺序存储和链式存储），数据操作（对数据结构中的元素进行各种运算和处理），而通常所说的算法是建立在数据结构之上，读数据结构的操作需要用算法来描述。而算法的分析又主要包括时间代价和空间代价两方面

线性表的顺序表示和实现

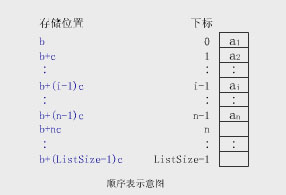
Alt text

数组是顺序存储的随机存取结构，占用一组连续的存储单元，通过下标识别元素，元素地址是下标的线性函数，一个下标能唯一确定一个元素
不妨构造一个顺序表接口类来模仿顺序表

1
2
3
4
5
6
7
8
9
10
11
12
13
public interface LList<T> {
	boolean isEmpty();       //判断线性表是否为空
	int length();            //返回线性表长度
	T get(int i);            //返回第i(i>=0)个元素
	void set(int i,T x);     //设置第i个元素值为x
	void insert(int i,T x);  //插入x作为第i个元素
	void append(T x);        //在线性表最后插入第i个元素
	T remove(int i);         //删除第i个元素并返回被删除对象
	void removeAll();        //删除线性表所有元素
	int indexOf(T key);      //顺序查找关键字为key的元素，返回首次出现的位置
	boolean contain(T key);  //是否包含关键字
	T search(T key);         //顺序查找关键字为key的元素，返回首次出现的元素
}

下面是其实现类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
public class seqList<T> implements LList<T>{
	private Object[] element; //存放线性表元素的一维数组
	private int len;       //顺序表长度，记载元素个数
	
	public seqList(int size){            //创建容量为size的空表
		//若size<0，java将抛出负数组长度异常
		this.element=new Object[size];
		this.len=0;
	}
	
	public seqList(){     //创建默认容量的空表，这里是64
		this(64);
	}
	
	public boolean isEmpty() {
		
		return this.len==0;
	}
	public int length() {
	
		return this.len;
	}
	public T get(int i) { //返回第i个元素（i>=0),若i指定元素无效，则返回null
	if(i>=0&&i<this.len)
		return (T)this.element[i];
    return null;
	}
	//设置第i(i>=0)个元素的值为x，若i指定序号无效则抛出序号越界异常
	public void set(int i, T x) {
		if(x==null)
			return;
		if(i>=0&&i<this.len)
			this.element[i]=x;
		else
			throw new IndexOutOfBoundsException(i+"");
		
	}
/**
 * 在顺序表元素ai位置插入元素x，首选必须将i到n个元素后移，空出一个位置，然后插入元素x
 */
	public void insert(int i, T x) {
		if(x==null)
			return ;           //不能添加null
		if(this.len==element.length)	 //若数组满，则扩充顺序表容量
		{ 
			Object[] temp=this.element;
			this.element=new Object[temp.length*2]; //容量扩充2倍
			for(int j=0;j<temp.length;j++){ 
				this.element[i]=temp[i];  //复制数组元素
			}
			if(i<0)                      //下标容错
				i=0;
			if(i>this.len)
				i=this.len;
			for(int j=this.len-1;j>=i;j--)       //元素后移，平均移动len/2
				this.element[j+1]=this.element[j];
			this.element[i]=x;
			this.len++;
		}
		
	}
	public void append(T x) {
		insert(this.len,x);	   //在顺序表最后插入x对象
	}
	
	/**
	 * 删除元素ai，必须将元素i+1到n向前移动
	 */
	public T remove(int i) { //删除成功返回被删除对象，否则返回null
		if(this.len==0||i<0||i>this.len)
			return null;
		T old=(T)this.element[i];
		 for(int j=i;j<this.len-1;j++)     //元素前移，平均移动len/2
			 this.element[j]=this.element[j+1];
		 this.element[this.len-1]=null;
		 this.len--;
		return old;
	}
	public void removeAll() {
		
		this.len=0;
	}
//顺序查找关键字为key的元素，返回首次出现的位置，若查找不成功返回-1
	public int indexOf(T key) {
		if(key!=null)
			for(int i=0;i<this.len;i++)
				if(this.element[i].equals(key))
					return i;
		return -1;
	}
	//判断线性表是否包含关键字为key元素
	public boolean contain(T key) {
		
		return this.indexOf(key)>=0;
	}
	//查找，返回首次出现的关键字为key的元素
	public T search(T key) {
	 int find=this.indexOf(key);
		return find==-1?null:(T)this.element[find];
	}
}

约瑟夫环问题

问题描述：古代某法官要判决n个犯人的死刑，他有一条荒唐的法律：将犯人站成一个圆圈，从第s个人开始数起，每数到第d个犯人，就拉出来处决，在从下一个开始数d个，数到的人在处决。。。直到数到最后一个人就开始赦免

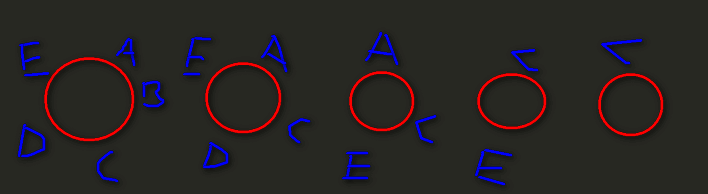
Alt text
上面是假设n=5，s=1，d=2，并且起始位置是从第一个人开始数起，因为该圆圈可以看成顺序表进行模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Josephus {
	public Josephus(int number,int start,int distance){
		seqList<String> list=new seqList<String>(number); //初始化顺序表
		for(int i=0;i<number;i++)                      
		//依次添加犯人，这里记为A,B.C,D,E
			list.append((char)('A'+i)+"");
		System.out.println("初始化约瑟夫环:"+'('+number+','+start+','+distance+')');
		int i=start;            //起始数起的人
		while(list.length()>1){        //多于一个犯人时数起
			i=(i+distance-1)%list.length(); 
			System.out.print("删除"+list.remove(i).toString()+"");
			System.out.println(list.toString());
		}
		System.out.println("最后的被赦免者是:"+list.get(0).toString());	
	}
	
	public static void main(String args[]){
		new Josephus(5,0,2);
	}
}

结果

初始化约瑟夫环:(5,0,2)
删除B(A,C,D,E)
删除D(A,C,E)
删除A(C,E)
删除E(C)
最后的被赦免者是:C

顺序表的效率分析

由之前的源码易看出，存取任何一个元素，即set（）、get（）方法的时间复杂度为O（1），而插入或者删除很耗时，不妨假设在第i个位置插入元素，并且概率为p{i},表长度为n；则平均移动次数为\sum{i=0}^n{(n-i)}*{p_i};
如果插入元素的概率相同，即都是1/(n+1);最后求得时间复杂度为O(n);同理删除的时间复杂度也为O(n);
所以得出一个结论:顺序表的动态操作效率极低

顺序表比较相等

首先简单说一下深拷贝和浅拷贝，浅拷贝类似于只引用某个对象，和原对象指向相同的空间，而深拷贝是开辟了新空间并且复制原来对象的数据
而两个顺序表的相等是指，他们对应的元素相等并且长度也相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public boolean equals(Object obj){
		if(this==obj)
			return true;
		if(obj instanceof seqList){
			seqList<T> list=(seqList<T>)obj;
			if(this.length()==list.length()){
				for(int i=0;i<this.length();i++)
					if(!(this.get(i).equals(list.get(i))))
						return false;
				return true;
			}
				
		}
			return true;
	
	}

快乐源于分享，总结溢于提高

热评文章